Digital Audio and the Mac
The Specifics of Sampling
Last month, we introduced the fundamentals of audio, analog representation, and digital representation. To review, an analog system allows a continuous variation in voltages which corresponds analogously to a continuous variation in air pressure. A digital system must make discreet measurements that approximate this continuum of values. The greater the number of measurements, the more accurate the result. The decision, therefore, is between accuracy and storage space.
Sample Rate
A sample is a single measurement of amplitude. The sample rate is the number of these measurements taken every second. In order to accurately represent all of the frequencies in a recording that fall within the range of human perception, generally accepted as 20Hz–20KHz, we must make sure that we choose a sample rate high enough to represent all of these frequencies. At first consideration, one might choose a sample rate of 20KHz since this is identical to the highest frequency. This will not work, however, because every cycle of a waveform has both a positive and negative amplitude and it is the rate of alternation between positive and negative amplitudes that determines frequency. Therefore, we need at least two samples for every cycle resulting in a sample rate of at least 40KHz. This principle is known as the Nyquist Theorem. It is usually stated as follows:
sample rate = 2 x highest frequency
or in another version:
N = 1/2(sample rate)
The Nyquist frequency (shown here as “N”) is therefore defined as one half of the sample rate and is the highest frequency that can be accurately represented. So given some standard sample rates, we can easily find the Nyquist frequency:
|
Media |
Sample Rate |
Nyquist Frequency |
|---|---|---|
|
CD Standard |
44.1KHz |
22.05KHz |
|
DAT (alternate) |
48KHz |
24KHz |
|
DVD |
96KHz |
43KHz |
In each case, the Nyquist frequency is above the highest frequency in the range of human hearing. What advantage is there in representing these extra ultrasonic frequencies?
An Aside on Filters
As you recall from Part I, a low-pass filter is used to smooth out the steps in the waveform. Frequencies within the range of human hearing pass through unaltered, while ultrasonic frequencies are attenuated. This attenuation increases a certain amount for every octave above the cutoff frequency (c) of the filter.
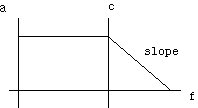
In general, a smooth slope yields a more natural sound. Much of the harshness attributed to early CDs, in fact, was due to sharp “brick wall” filters. So given a fixed cutoff frequency (around 19KHz), a higher Nyquist frequency allows for a smoother slope.
Aliasing (or Foldover)
What exactly happens to frequencies that lie above the Nyquist frequency? First, we’ll look at a frequency that was sampled accurately:

In this case, there are more than two samples for every cycle, and the measurement is a good approximation of the original wave. A low-pass filter will smooth out the steps and we will get back the same signal we put in. If we undersample the signal, though, we will get a very different result:
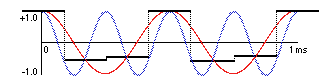
In this diagram, the blue wave is the original frequency. The red wave is the aliased frequency produced from an insufficient number of samples. This frequency, which was in all likelihood a high partial in a complex timbre, has folded over and is now below the Nyquist frequency. For example, a 11KHz frequency sampled at 18KHz would produce an alias frequency of 7KHz. This will alter the timbre of the recording in an unacceptable way.
Sample Resolution
Each sample can only be measured to a certain degree of accuracy. The accuracy is dependent on the number of bits used to represent the amplitude, which is also known as the sample resolution. The sample resolution determines the optimal signal to noise ratio of the digital medium in question as follows:
8-bit (X 6) = 48db SNR
12-bit (X 6) = 72db SNR
16-bit (X 6) = 96db SNR
24-bit (X 6) = 144db SNR
To put these numbers in perspective, consider the following: the dynamic range of human hearing from the threshold of perception to the threshold of pain is between 130 and 140db. In contrast to that, the dynamic range of high quality audio tape is around 70db and the dynamic range of CDs (16 bit) is 96db. DVD, however, has a sample resolution of 24 bits, allowing it theoretically to capture the full dynamic range of acoustic music.
The other point to consider is that every six decibels adds one bit to the sample resolution. Why is this important? Because, if the hottest signal in a 16-bit recording is at -6db (with 0db the loudest signal the system can represent) the result is the same as a 15-bit recording with the hottest signal at 0db. In fact, if you normalized this file (raising the highest amplitude to 0db), the result would be identical to a 15-bit recording.
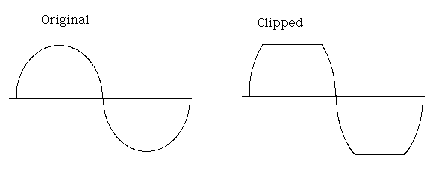
Clipping
Both analog and digital media have an upper limit beyond which they can no longer accurately represent amplitude. Analog clipping (or overdrive or distortion) varies in quality depending on the medium. A tube amplifier, for example, has a much warmer distortion than a solid state amplifier. In each case the upper amplitudes are being altered, distorting the waveform and changing the timbre, but the alterations are slightly different. Digital clipping, in contrast, is always the same. Once an amplitude of 1111111111111111 (the maximum value in a 16 bit resolution) is reached, no higher amplitudes can be represented. The result is not the smooth, rounded flattening of analog clipping, but a harsh slicing of off the top of the waveform, and an unpleasant timbral result.
An Ideal Recording
We should all strive for an ideal recording. Based upon what we’ve covered so far, we can draw some basic conclusions that will help us reach this goal. First, don’t ignore the analog stage of the process. Use a good microphone, careful microphone placement, high quality cables, and a reliable analog-to-digital converter. Strive for a hot (high levels), clean signal. After all, a CD-quality sample of a cheap cassette sounds no better than the cheap cassette itself. Second, when you sample, try to get the maximum signal level as close to zero as possible without clipping. That way you maximize the inherent signal-to-noise ratio of the medium. Third, avoid conversions to analog and back if possible. You may need to convert the signal to run it through an analog mixer or through the analog inputs of a digital effects processor. Each time you do this, though, you add the noise in the analog signal to the subsequent digital reconversion.
Next Month: Digital Audio and the Mac—Part III: Software.
Also in This Series
- Digital Audio on the Internet · June 2000
- Hardware · May 2000
- Software · April 2000
- The Specifics of Sampling · March 2000
- Fundamentals · February 2000
- Complete Archive
Reader Comments (17)
=20*log(256)
=20*2.4
=48.16 dB, which is the correct answer. (You can check that my formula works out for the other SNR values quoted above.) The reason why 20*log(I/I0) is used in audio instead of 10*log(I/I0) is so that 10 dB will roughly correspond to "twice as loud." I think that this departure from conventional notation is a bad idea, but what can I do? 6*resolution is a great approximation for max SNR (6.02*resolution is even better.) Here is the derivation:
20*log(2^resolution)
=20*log(2)*resolution
~=6.02*resolution
I have used the fact that log(x^y)=y*log(x), and 20*log(2)~=6.02. Just in case anyone isn't familiar with my notation:
^ means "to the power of"
log means "log base 10"
~= means "approximately equal to"
* means "multiplied by"
Cheers, Chris
The reason why 20*log(I/I0) is used in audio instead of 10*log(I/I0) is so that 10 dB will roughly correspond to "twice as loud."
I believe 20*log(ratio) is used for voltage ratios, while 10*log(ratio) is used for power, because power=voltage^2/resistance. Since Audio measurements are usually of voltage, not power, 20 is the appropriate multiplier.
What sounds "twice as loud", however, is subjective, and depends on frequency (c.f. Fletcher-Munson).
That my dear friend is the only correct answer. :) I always wonder why also I myself didn't know this until about a year ago. I'm a student electronical engineering and in our courses of analog electronics I never figured it out until I actually started looking through references. Anyway, now it should be clear for all of us. :-)
at 8 bit or at 24 bit the maximum level is the same ( the headroom)
Ex.at the both bitrata the ADC hase the same maximum voltage
.At 8 bit the signal can have 256 subdivision of the maximum level this is the amplitude resolution.
At 24 bit we can have 2^24(16,777,216) subdivision of the amplitude .is more higher resolution.we can
If The maximum handled voltage ( signal) is the same , both ADC cliping at the same overdrive level .Ex:,If the max voltage of signal is 5 V both ADC at 6 bit and at 24 bit or 32 bit or 64 bit cliping at bigger voltage then 5V .
The higher bitrata is good for the beter resolution of amplitude so ADC can falow very small signal changes of the audio program , so we have higher fidelity .Other good thing is , the insertion noise is smaller because of very small steping in amplitude we have small steps in amplitude "sampling " , this can filter easier.
Whith Nyquist frecvency , i think is for just one single sinus waveform .
I read in book abaut TV , for shynthesis of one square waveform we need to mix up too the #21 harmonics, so the harmonics #21 component is very high freqency and i think we need to have sampling rata for this (?)if we need really HI-FI conversion.
( ecscuse my poor english)
1. find the highest and smallest number that can be stored .
2. find the error if it exist
http://www.samsontech.com/products/productpage.cfm?prodID=1810
The specifications say:
-16-bit sample resolution
-Supports 8 kHz, 11.025 kHz, 22.05 kHz, 44.1 kHz, and 48 kHz sampling rates
I have read some advice about increasing the software's recording sample to 24-bit when recording onto computer. But if the mic's specs state 16-bit resolution, is there any point (or advantage) in recording it to 24-bit? Or will it be unaffected leaving the recording at 16-bit, since the resolution of the mic is 16-bit to begin with?
Any advice on this would be much appreciated!
May be this will help you:
http://www.knowledgerush.com/kr/jsp/db/board.jsp?id=54913
http://www.ieindia.org/pdf/88/88ET104.pdf
http://www.ieindia.org/pdf/89/89CP109.pdf
http://www.pueron.org/pueron/nauchnakritika/Th_Re.pdf
http://www.radiotec.ru/catalog.php?cat=jr4&art=2363
http://www.radiotec.ru/catalog.php?cat=jr4&art=2308
Good luck!
Best regards
Petre Petrov
Add A Comment